Quantum Non-Locality and Relativity: Chapter 1

Introduction

The book opens with an introduction that teases us with some of the ideas that will be developed later on. We start with a statement of Bell’s theorem:

…observable correlations between [entangled] particles could not be accounted for by any theory which attributes only locally defined physical states to them. The particles appear to be ‘connected’ or “in communication” no matter how distantly separated they may become. The outcome of experiments performed on one member of the pair appears to depend not just on that member’s own intrinsic physical state, but also on the result of the experiments carried out on its twin.

Of course, the results described above are in tension with the theory of Relativity, we all know that. Maudlin goes on to point out that the constraints of Relativity are both well understood in that “things” are not permitted to travel faster than light. What those things are is up for debate. He distinguishes the candidates:

• Matter or energy cannot be transported faster than light
• Signals cannot be sent faster than light
• Causal processes cannot propagate faster than light
• Information cannot be transmitted faster than light

These are not necessarily equivalent, which I think I agree with. For example, one could imagine sending matter/energy faster than light but only if it has no information content. This requires two of the rules state above. I would consider Signals and Information to be the same thing, but perhaps they are specific terms of art?

More interestingly, Maudlin then brings up another interpretation of Relativity that I don’t think I’ve encountered:

• Theories must be Lorentz invariant

And points out that Lorentz invariant theories don’t forbid anything in the four-item list above. This last statement surprised me, since I always thought of Lorentz invariance as a property that relativistic theories have as a consequence of the stronger prohibitions against superluminal causality and superluminal matter/energy/signals propagation. I discussed this with my colleagues and they seemed to believe that the first four prohibitions are consequences of Lorentz invariance, so it looks like I’ll be dusting off my Special Relativity textbook as we go through the following chapters.

Regardless, we are promised that each of the prohibitions above, their justifications, and their relations to each other will be discussed later in the book.

The last (most important?) part of the Introduction is in its only footnote. Maudlin points out that this book requires only the assumption that something in the universe picks out the results we measure vs all other possibilities. He notes that this permits basically all major interpretations of quantum mechanics except for Everett’s Many Worlds Interpretation (MWI) and something called “many minds”.

Amusingly, he asserts that the MWI is ‘incoherent’ because it does not yield probabilities when branches split. I’ve seen proponents of MWI assert with just as much conviction that it is the ‘obviously’ correct interpretation. I plan on returning to MWI by reading the source material in some later post.

So that’s the introduction. We are told that there are some empirically validated results in quantum mechanics that seem to violate some physical prohibitions imposed on us by Relativity. Except it turns out maybe we’re not quite sure what Relativity really is prohibiting at all?

With that set-up, we move on to chapter 1: Bell’s Theorem.

Chapter 1: Bell’s theorem

The chapter opens with an excerpt of a letter from Albert Einstein to Max Born that basically boils down to Einstein arguing that “things” are “real” and also “separate”. Without such distinctions between “real” and “separate” “things”, physical thinking (thinking about physics) would not be possible.

I found myself agreeing that things are indeed real and separate, but am worried that we are maybe in for a nasty surprise. Perhaps things are not real? Or worse, not separate?

The rest of the chapter lays out a simplified version of Bell’s result, then an increasingly refined series of thought experiments where you and a friend play the role of entangled photons emitted by a calcium (\(Ca^+\)) ion.

In these thought experiments, we seek to reproduce the behavior of a real \(Ca^+\) ion and its emitted photons. In the real thing, the calcium ion emits two photons simultaneously toward two different polarizers. The polarizer orientations are selected at random from a limited set of angles, 0, 30, and 60 degrees. Behind each polarizer is a photon detector so we can measure whether a photon passed through, or was absorbed by the polarizer. What quantum mechanics tells us is that the probability of both detectors measuring a photon is a simple function of the difference in polarization angle between the polarizers. If \(\theta_1\) is the angle of the first polarizer, and \(\theta_2\) is the angle of the second polarizer, then we can define \(\alpha = \theta_1 - \theta_2\). The probability of both detectors measuring a photons is then just \(P = \cos^2\left(\alpha\right)\).

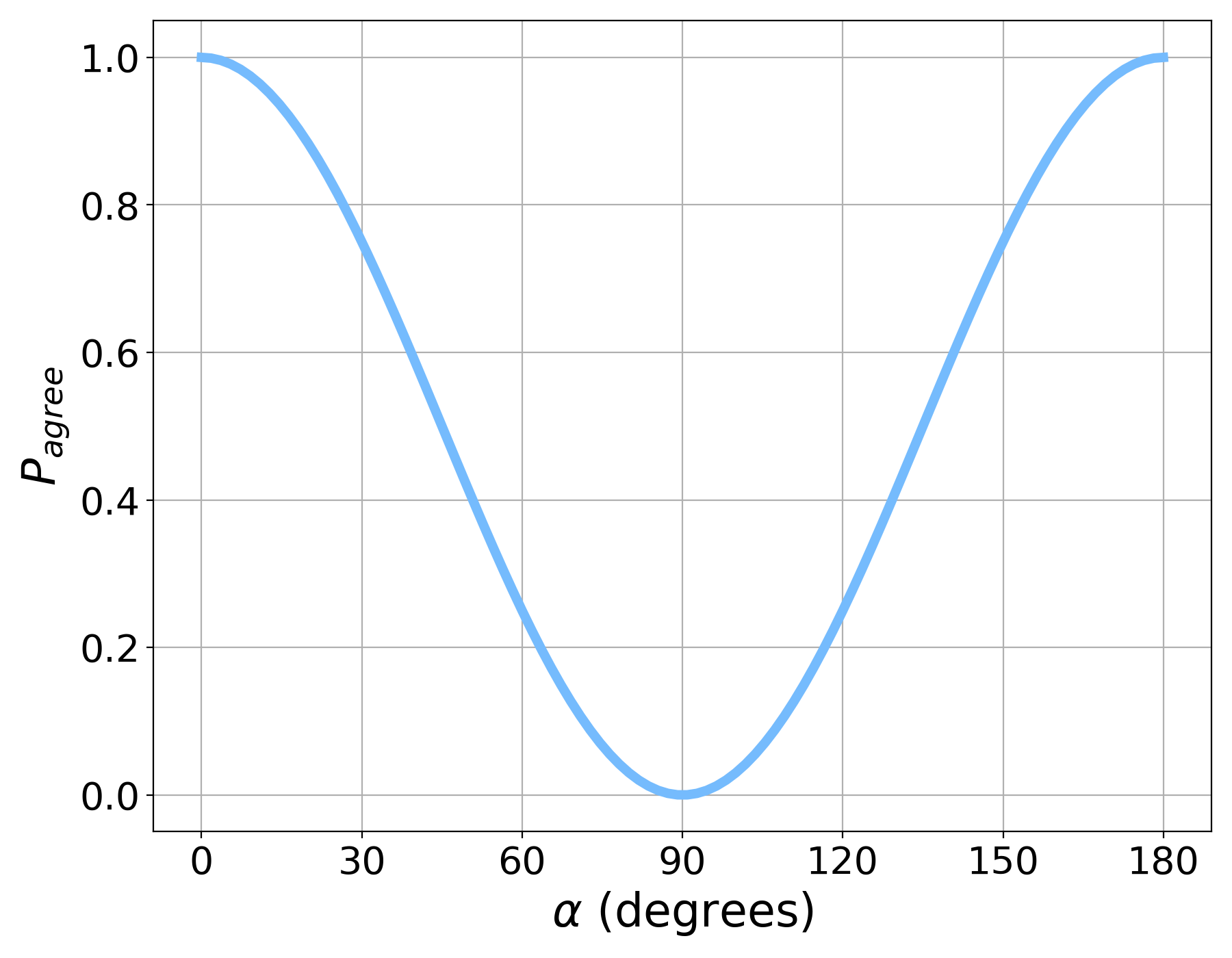
In order to agree with quantum mechanics, your answers must adhere to three conditions:

Fact 1: When you and your friend are asked the same question, you must give the same answer.

Fact 2: When you and your friend are asked questions that differ by \(30^{\circ}\), your answers must agree \(\frac{3}{4}\) of the time.

Fact 3: When you and your friend are asked questions that differ by \(60^{\circ}\), your answers must agree of the time.

At this point I invite you to try out some strategies. You will find that it is impossible to satisfy all three conditions. The sample strategies that Maudlin advances can be agreed upon before-hand by the participants, guaranteeing Fact 1 will remain true. Attempting to satisfy Facts 2 & 3 will result in incoherent results, like negative percentages.

After reading this section, I wanted to make sure my quantitative understanding of Bell’s theorem was correct, so first I went to the source, Bell’s 1964 paper. It is mercifully short, but also a little bit opaque to me, a humble experimental physicist. I usually like to see at least one worked out example, so I went and found one:

The last thing I’ll say about Maudlin’s thought experiment, is that I always considered entangled particles ‘one thing’. That seems like an important distinction, especially because this non-locality problem doesn’t become apparent until you compare all detector results! Merely measuring one part of the entangled system just gives random results, as you would expect. The need to have collected information about all parts of the entangled system seems important to me, but I’m not sure why or how. Hopefully this will be addressed further in the book.

The final part of this chapter is a nice list about why this entanglement is weird.

1. The quantum connection is unattenuated

All of the fundamental forces, which are the source of interactions between objects, have some dependence on separation. Gravitational and electromagnetic forces lessen proportional to the inverse square of distance (\(F \sim \frac{1}{r^2}\)). The more exotic forces, Weak and Strong, have even stronger dependence on distance, which is why their effects dominate only on the subatomic level. Entanglement, however, has no distance depenence. Two particles will be just as entangled 1 micron apart as they would be 100 lightyears apart. Quantum mechanics does not offer a prediction that the correlations we find so troubling would decay with increased distance.

2. The quantum connection is discriminating The quantum connection depends on history. Only particles which have interacted with each other in the past seem to retain this power of private communication. No classical force exhibits this kind of exclusivity.

I am less comfortable with this statement. The discrimination actually seems to be exclusively a human problem. The modern description of the fundamental forces says that they are mediated by particles, which for ‘undiscriminating’ forces are simply being exchanged between all objects all the time. This suggests that entanglement is just a product of our limited ‘book-keeping’ when it comes to physics. If we were able to monitor all correlations of every particle in the universe, would it all just look entangled? Since we can’t do this, we only track correlations between very limited collections of particles, it looks like entanglement is special.

3. The quantum connection is faster than light (instantaneous)

As we’ll see, experimental realizations of Bell’s Theorem try very hard to make their separated measurements simultaneously. As far as I know, the empirical upper bound on the speed on this communication between entangled particles is \(\gg c\). As we’ll see, the theory of relativity makes the word “simultaneous” ill-defined in certain circumstances, but even that will not save us.